Mithilfe einer tragbaren Rechenmaschine ist es mir gelungen, unter knapp 260 verdächtigen Personen in den Kolonien den Gefährder Paul Revere auszumachen. Eine Demonstration der neuesten Errungenschaften auf dem Gebiete der Rechenkun?t.
London, 1772
Meine Vorgesetzten ersuchten mich, kurz und knapp die vortreffliche Leistungsfähigkeit der simpelsten Methoden der neumodischen sozialen Netzwerkanalyse zu demonstrieren, mit der wir jenen auf die Spur kommen können, die danach trachten, die von den Untertanen Seiner Majestät genossene Freiheit zu unterminieren.
Dies steht im Zusammenhang mit der Debatte über die Rolle von „Metadaten“ bei gewissen Vorkommnissen in jüngerer Vergangenheit und der Versicherung verschiedener respektabler Beteiligter, dass die Regierung nichts weiter täte, als „diese sogenannten Metadaten zu durchsieben“ und dass „mit den gesammelten Daten nicht die Inhalte der Gespräche erfasst würden“. Ich werde zeigen, wie wir diese „Metadaten“ nutzen können, um Schlüsselgestalten aufzuspüren, die sich in terroristischen Gruppen betätigen, welche derzeit in den Kolonien ihr Unwesen treiben. Ich werde mich auch darum bemühen, darzulegen, wie diese Methoden in einer Art und Weise wirken, die man als relational bezeichnen könnte.
Die Analyse in diesem Bericht beruht auf den Daten, die unser Repräsentant vor Ort – Mr. David Hackett Fischer – sammelte und im Anhang seines ausführlichen Berichts an die Regierung veröffentlichte. Wie Sie vielleicht wissen, ist Mr. Fischer ein angesehener Repräsentant mit breiten und fundierten Kenntnissen über die Kolonien. Ich selbst dagegen habe mich hochgearbeitet; in Irland hatte ich nur eine kurze quantitativ-methodische Ausbildung absolviert und während meiner Zeit in Cambridge rangierte ich in der Bestenliste der Mathematikstudenten der höheren Semester mehrere hundert Plätze hinter dem Erstplatzierten.
Jetzt arbeite ich als analytischer Skribent von niederem Rang in der guten alten National Security Agency – ich bitte um Nachsicht, ich meine natürlich die Royal Security Agency (RSA). Und ich möchte nicht versäumen, nochmals kundzutun, dass ich nichts über die derzeitigen Vorkommnisse in den Kolonien weiß. Unsere aktuelle, in diesem unseren 18. Jahrhundert entwickelte Beta-Version von PRISM wurde jedoch dazu genutzt, Daten von knapp 260 mehr oder weniger verdächtigen Personen, die sieben verschiedenen Organisationen im Raum Boston angehören, zu sammeln und zu analysieren.
Seien Sie versichert, dass wir ausschließlich Metadaten über diese Personen sammelten, dass keine Gespräche auf Versammlungen mitgeschrieben wurden. Meine Kenntnisse beschränken sich darauf, ob jemand Mitglied einer Organisation war oder nicht. Das ist doch nun wirklich nur ein kleiner Eingriff in die Freiheitsrechte der Untertanen der Krone! Ich wurde beauftragt, anhand dieser spärlichen Daten einige Namen herauszufinden, denen unsere Repräsentanten in den Kolonien nachgehen können. Dies scheint eine nicht ganz leichte Aufgabe.
Wenn Sie das ganze Unterfangen mit verfolgen wollen, gibt es ein geheimes Repositorium, in dem alle Daten und entsprechenden Befehle für Ihre tragbare Rechenmaschine enthalten sind. Und so sehen unsere Daten aus (siehe Tab. 1):
| St Andrews Lodge | Loyal Nine | North Caucus | Long Room Club | Tea Party | Boston Commit tee | London Enemies | |
|---|---|---|---|---|---|---|---|
| Adams. John | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| Adams. Samuel | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| Allen. Dr. | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Appleton. Nathaniel | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| Ash. Gilbert | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Austin. Benjamin | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Austin. Samuel | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Avery. John | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| Baldwin. Cyrus | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Ballard. John | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
Tabelle 1: Mitgliedschaften in Organisationen
In den Spalten sind die Organisationen aufgelistet und in den Zeilen die Namen der Personen. Die Mitgliedschaft wird durch eine „1“ angezeigt. Also ist ein gewisser Samuel Adams (wer auch immer er sein mag) Mitglied im North Caucus, im Long Room Club, im Boston Committee und bei der London Enemies List. Ich muss sagen, dass die Namen dieser Organisationen recht kampfeslustig klingen.
Was können wir aus diesen dürftigen Metadaten überhaupt erschließen? Diese Tabelle ist groß und sperrig und ich bin nur ein kleiner Angestellter in der guten alten RSA, weshalb ich mich nur schlichter Mittel bedienen kann. Ich bin ziemlich sicher, dass meinen Vorgesetzten viel ausgereiftere analytische Methoden zur Verfügung stehen. Ich folge nun einer Methode, die mein hervorragender einstmaliger Kollege Ron Breiger in einer Abhandlung mit dem Titel „The Duality of Persons and Groups“ dargelegt hat. Er verfasste dieses Papier vor etwa 35 Jahren als Doktorand in Harvard. (Sie erinnern sich vielleicht, dass Harvard in den Kolonien als Universität angesehen war. Egal.)
In dem Papier wird das beschrieben, was heute als Grundmethode der Datenrepräsentation gilt, mit der Daten über Verbindungen zwischen Menschen und anderen Dingen dargestellt werden – wie etwa die Teilnahme an Veranstaltungen oder die Mitgliedschaft in Gruppierungen. In dieser neuen Wissenschaft geht es in der Tat fast immer darum, was man über Personen ausschließlich anhand von Metadaten aussagen kann, ohne auf Äußerungen dieser Personen einzugehen.
Mr. Breigers Erkenntnis bestand darin, dass unsere Tabelle aus 254 Zeilen und sieben Spalten eine sogenannte Nachbarschafts- oder Adjazenzmatrix ist und dass ein wenig Multiplikation Daten hervorbringen kann, die in der Tabelle stecken, aber möglicherweise nur schwer zu erkennen sind. Nimmt man diese Matrix und dreht sie so um, dass die Zeilen zu Spalten werden und umgekehrt, so hat man zwei Tabellen oder Matrizen: Erstens eine 254×7-Tabelle, in der die Namen in Zeilen den Organisationen in Spalten gegenüberstehen. Zweitens eine 7×254-Tabelle, in der die Organisationen in Zeilen und die Namen in Spalten dargestellt sind.
Nennen wir die erste Adjazenzmatrix A und die transponierte Matrix AT. Nun gibt es, wie Sie sich vielleicht erinnern, Regeln für die Multiplikation von Matrizen. Das Ausmultiplizieren von A(AT) ergibt eine große Matrix von 254 Zeilen und 254 Spalten, in der sowohl die Zeilen als auch die Spalten Personen sind und die Ziffern in den Zellen die Anzahl der Organisationen angibt, in denen beide Männer des jeweiligen Personenpaares Mitglied sind. Ist das nicht wunderbar? Ich habe immer das Gefühl, diese Operation grenzt an Zauberei, insbesondere weil sie damit einhergeht, eine Hand von oben nach unten und die andere von links nach rechts zu bewegen, was einer Beschwörungsgeste ähnelt.
Ich kann Ihnen die gesamte Personen-gegenüber-Personen-Matrix nicht zeigen, weil ich Sie damit erschlagen würde. Nur ein Scherz, nur ein Scherz! Aber sie ist tatsächlich ziemlich groß. Sehen Sie hier einen kleinen Ausschnitt davon (siehe Tab. 2). Wir können eine solche 254×254-Matrix als Bigge Data bezeichnen. Ich werde demnächst einen EDWARDx-Vortrag darüber halten. Sie sollten kommen!
Zurück zur Matrix:
| Adams. John | Adams. Samuel | Allen. Dr. | Appleton. Nathaniel | |
|---|---|---|---|---|
| Adams. John | - | 2 | 1 | 1 |
| Adams. Samuel | 2 | - | 1 | 2 |
| Allen. Dr. | 1 | 1 | - | 1 |
| Appleton. Nathaniel | 1 | 2 | 1 | - |
| Ash. Gilbert | 0 | 0 | 0 | 0 |
| Austin. Benjamin | 0 | 1 | 0 | 0 |
Tabelle 2: Personen-gegenüber-Personen-Matrix
Man sieht, dass Mr. Appleton und Mr. John Adams dadurch miteinander verbunden sind, dass sie beide derselben Organisation angehören, während Mr. John Adams und Mr. Samuel Adams sogar in zwei unserer sieben Gruppen gemeinsam Mitglied sind. Mr. Ash stand dagegen mit keinem der vier erstgenannten Männer durch Mitgliedschaft in derselben Organisation in Verbindung.
Führen Sie sich das noch einmal vor Augen! Wir begannen nicht mit einem sozialen Netzwerk, in dem Einzelpersonen miteinander verbunden sind. Unser Ausgangspunkt war eine Liste von Mitgliedschaften in mehreren Organisationen. Aber jetzt haben wir plötzlich ein soziales Netzwerk von Einzelpersonen, in dem die Verbindung durch die gemeinsame Mitgliedschaft in einer Organisation definiert ist. Das ist ein wahrlich großmächtiger Zaubertrick.
Und dabei fangen wir gerade erst an. Bei der Multiplikation von Matrizen ist zu beachten, dass die Reihenfolge eine Rolle spielt; es ist daher nicht wie bei der Multiplikation von zwei Zahlen. Wenn wir bei der Multiplikation die transponierte Matrix an die erste Stelle setzen, bekommen wir ein anderes Ergebnis. Aus dieser Multiplikation ergibt sich eine 7×7-Matrix der Organisationen. Die Ziffern in den Zellen zeigen, wie viele Personen jedes Organisationspaar gemeinsam hat. Und das sieht dann so aus. Da diese Tabelle klein ist, können wir sie in ihrer Gesamtheit betrachten.
| St Andrews Lodge | Loyal Nine | North Caucus | Long Room Club | Tea Party | Boston Commit-tee | London Enemies | |
|---|---|---|---|---|---|---|---|
| St Andrews Lodge | - | 1 | 3 | 2 | 3 | 0 | 5 |
| Loyal Nine | 1 | - | 5 | 0 | 5 | 0 | 8 |
| North Caucus | 3 | 5 | - | 8 | 15 | 11 | 20 |
| Long Room Club | 2 | 0 | 8 | - | 1 | 5 | 5 |
| Tea Party | 3 | 5 | 15 | 1 | - | 5 | 10 |
| Boston Committee | 0 | 0 | 11 | 5 | 5 | - | 14 |
| London Enemies | 5 | 8 | 20 | 5 | 10 | 14 | - |
Tabelle 3: Verbindungen zwischen Organisationen
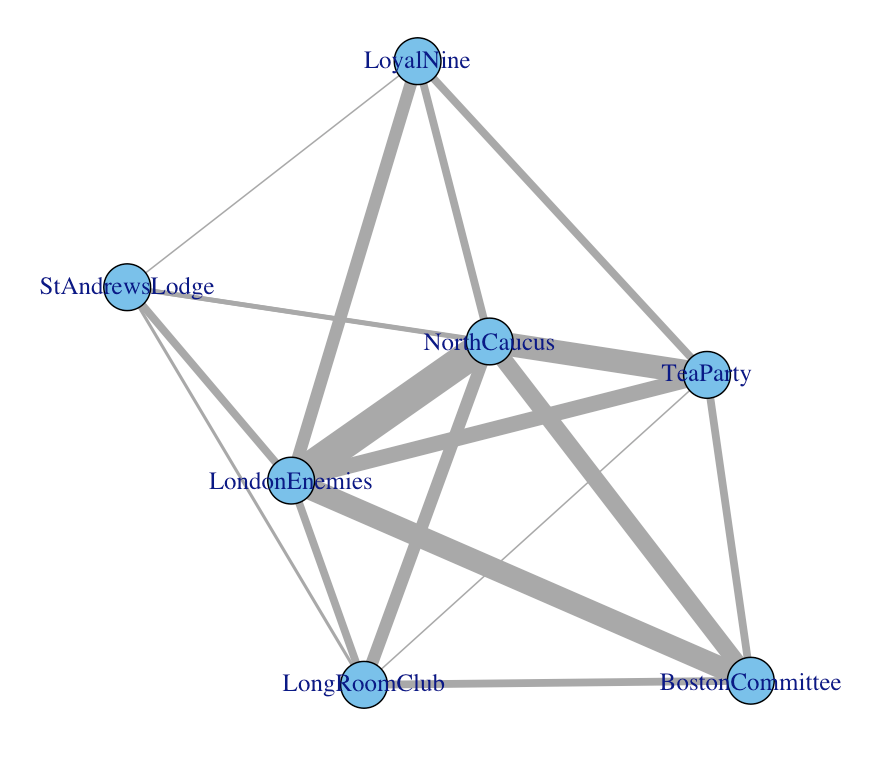
Auch interessant! Statt zu sehen, welche Personen durch gemeinsame Mitgliedschaft in Organisationen miteinander verbunden sind, sehen wir hier, welche Organisationen durch Personen miteinander verbunden sind, die beiden Gruppierungen angehören. Personen sind also durch Gruppen, denen sie angehören, miteinander verbunden. Gruppen sind durch die Personen, die sie gemeinsam haben, miteinander verbunden. Das ist die im Titel von Mr. Breigers Abhandlung genannte „Dualität von Personen und Gruppen“.
Statt sich nur auf Tabellen zu stützen, können wir auch ein Bild der Beziehungen zwischen den Gruppen malen, indem wir die Anzahl der gemeinsamen Mitglieder als Index der Stärke der Verbindung zwischen den aufwieglerischen Gruppen nutzen. Das sieht dann so aus:
Natürlich können wir auch die Verbindungen zwischen den Personen auf diese Weise darstellen, indem wir die 254×254-Tabelle nutzen. Daraus ergibt sich folgendes Bild:
Was für ein schönes Bild! Die Rechenmaschine hat alle Personen übersichtlich angeordnet und dabei Cluster von Individuen entdeckt. Es werden sowohl am Rand stehende Personen gezeigt als auch – viel spannender! – Menschen, die eine Verbindung zwischen verschiedenen Gruppen herstellen und daher für die nationale Sicherheit relevant sein könnten. Sehen Sie die Person, die ganz in der Mitte steht. Dieser Mann scheint auf ungewöhnliche (wenn auch vielleicht nicht einzigartige) Weise eine Brücke über mehrere Gruppen zu schlagen. Sein Name ist Paul Revere.

Paul Revere (1735-1818) war Silberschmied, Buchdrucker, Grafiker und US-amerikanischer Revolutionär. Seine Rolle als Nachrichtenkurier für die „Bostoner Patrioten” im Unabhängkeitskrieg machte ihn zum Nationalhelden. Bekannt wurde auch sein Kupferstich des „Boston Massacre” (s.o.).
Ich möchte Sie nochmals daran erinnern, dass ich nichts über Mr. Revere weiß, weder über seine Gespräche noch über seine Gewohnheiten, Überzeugungen und auch seine Schriften (wenn es denn welche geben sollte). Alles, was ich weiß, ist dieses Quäntchen an Metadaten. Und doch scheint meine Rechenmaschine aus unseren 254 Namen ihn als Person von besonderem Interesse herausgefischt zu haben.
Wir müssen uns hier nicht mit einem Bild begnügen. Jetzt, wo wir unsere Tabelle ausgewertet haben, um eine „Person-gegenüber-Person“-Matrix zu erzeugen, können wir weitere Operationen durchführen: Zentralitätsmaße berechnen; herausfinden, ob es Banden und Rotten gibt und andere Muster untersuchen. Beispielsweise könnten wir für jede Person in unserer Matrix ein „Intermediations-Zentralitätsmaß” errechnen, das ungefähr der Anzahl der kürzesten Wege zwischen jeweils zwei Personen in unserem Netzwerk entspricht, die über die verdächtige Person verlaufen. Es ist eine Fragestellung der Art „Wenn ich von Person A zu Person Z muss, wie wahrscheinlich ist es, dass der kürzeste Weg über Person X verläuft?“ Hier die höchsten Intermediationsmaße für unsere Liste mutmaßlicher Terroristen.
| >round(btwn.person[ind][1:10].0) | |||
|---|---|---|---|
| Revere. Paul | Urann. Thomas | Warren. Joseph | Peck. Samuel |
| 3839 | 2185 | 1817 | 1150 |
| Barber. Nathaniel | Cooper. William | Hoffins. John | Bass. Henry |
| 931 | 931 | 931 | 852 |
| Chase. Thomas | Davis. Caleb | ||
| 852 | 852 |
Tabelle 4: Betweenness-Zentralität
Vielleicht sollte ich ja nicht so voreilig von Terroristen reden. Aber Sie verstehen sicherlich, dass die Versuchung groß ist. Und siehe da – hier ist wieder unser Mr. Revere! Sehr interessant! Es gibt auch raffiniertere Wege als diesen, die Wichtigkeit einer Person in einem Netzwerk zu messen. Beispielsweise ist da die sogenannte „Eigenvektor-Zentralität”, über die mir meine Freunde aus der Naturphilosophie erzählen, sie sei ein kleiner Teil der Mathematik, der vermutlich nie eine praktische Anwendung in der weiten Welt finden werde. Man kann sie sich als ein Maß der Zentralität vorstellen, das durch die Verbindung zu anderen zentralen Personen gewichtet wird. Unsere Spitzenreiter nach diesem Maß sind:
| >round(cent.eig$vector[ind][1:10].2) | |||
|---|---|---|---|
| Barber. Nathaniel | Hoffins. John | Cooper. William | Revere. Paul |
| 1,00 | 1,00 | 1,00 | 0,99 |
| Bass. Henry | Davis. Caleb | Chase. Thomas | Greenleaf. William |
| 0,95 | 0,95 | 0,95 | 0,95 |
| Hopkins. Caleb | Proctor. Edward | ||
| 0,95 | 0,90 |
Tabelle 5: Eigenvektor-Zentralität
Auch hier erscheint unser Mr. Revere neben einigen anderen verdächtigen Personen oben auf der Liste. Als letzte Demonstration widme ich mich kurz der Berechnung von Macht und Zentralität nach Bonacich, einem höher entwickelten Messverfahren. Hier zeigt ein niedrigerer Wert eine zentrale Stellung an.
| >round(cent.bonpow[ind][1:10].2) | |||
|---|---|---|---|
| Revere. Paul | Urann. Thomas | Warren. Joseph | Proctor. Edward |
| -1,51 | -1,44 | -1,42 | -1,40 |
| Barber. Nathaniel | Hoffins. John | Cooper.William | Peck. Samuel |
| -1,36 | -1,36 | -1,36 | -1,33 |
| Davis. Caleb | Chase. Thomas | ||
| -1,31 | -1,31 |
Tabelle 6: Bonacich-Zentralität
Und wieder taucht Mr. Revere – neben den Herren Urann, Proctor und Barber – ziemlich weit oben auf unserer Liste auf.
Da haben wir es. Aus einer Tabelle über die Mitgliedschaft in verschiedenen Gruppen lassen sich diverse Dinge eruieren: ein Bild des sozialen Netzwerks zwischen Individuen, Hinweise auf den Grad der Verbundenheit zwischen Organisationen und einige klare Anhaltspunkte, wer in diesem Zusammenhang die wichtigsten Akteure sind. Und all das – wirklich alles! – anhand von ein paar Metadaten.
Ich möchte den meinen Auftragsrahmen nicht überschreiten, aber ich muss Sie doch bitten, sich vorzustellen, was möglich sein könnte, wenn wir erst in der Lage wären, Daten über sehr viel mehr Menschen zu sammeln und Daten aus verschiedenen Arten von Verbindungen zwischen Menschen zusammenzufassen! Denn die hier von mir beschriebenen einfachen Methoden sind auf andere Analysen übertragbar; ihre Leistungsfähigkeit wird mit dem Umfang und der Bandbreite der zu verarbeitenden Daten noch besser erkennbar. Wir müssten nicht wissen, was zwischen den Individuen geflüstert wurde, nur dass sie auf verschiedene Arten miteinander verbunden sind. Die Rechenmaschine würde den Rest erledigen!
Ich wage daher zu behaupten, dass die Form und Struktur der sozialen Beziehungen nach und nach aus unseren Berechnungen ersichtlich werden, zuerst lediglich als Umriss, aber schließlich immer deutlicher und zum Schluss in wunderschönen Einzelheiten – wie ein großes, lautloses Schiff, das aus dem grauen Nebel Neuenglands auftaucht. Ich räume ein, dass es neben der Möglichkeit, etwas Interessantes herauszufinden, auch dazu kommen könnte, dass sich suggestive, aber letztlich unrichtige und irreführende Muster herauskristallisieren. Ich glaube aber, dass diese Problematik gewiss durch größere und bessere Datenmengen weitgehend ausgeräumt werden wird.
Momentan verfügen wir noch nicht über die für eine automatische Sammlung der nötigen Daten erforderlichen Werkzeuge. Aber ich sage es noch einmal: Wenn ein bloßer Schreiberling wie ich die einfachsten dieser Methoden einsetzen kann, um den Namen eines Verräters wie Paul Revere unter 254 anderen Namen herauszupicken – indem er sich nichts weiter als eine Liste von Mitgliedschaften und eine tragbare Rechenmaschine zunutze macht – dann stelle man sich nur vor, welche Waffen uns in ein oder zwei Jahrhunderten zum Schutze der Freiheit zur Verfügung stehen werden.
 Kieran Healy ist Professor für Soziologie an der Duke University in Durham, North Carolina und arbeitet unter anderem am Duke Network Analysis Center. Zu seinen Veröffentlichungen gehört „Last Best Gifts, Altruism and the Market for Human Blood and Organs”. Der Artikel erschien zuerst auf kieranhealy.org, aus dem Englischen von Ina Goertz.
Kieran Healy ist Professor für Soziologie an der Duke University in Durham, North Carolina und arbeitet unter anderem am Duke Network Analysis Center. Zu seinen Veröffentlichungen gehört „Last Best Gifts, Altruism and the Market for Human Blood and Organs”. Der Artikel erschien zuerst auf kieranhealy.org, aus dem Englischen von Ina Goertz.
Dieser Text ist auch im Magazin „Das Netz – Jahresrückblick Netzpolitik 2013-2014“ erschienen. Sie können das Heft für 14,90 EUR bei iRights.Media bestellen. „Das Netz – Jahresrückblick Netzpolitik 2013-2014“ gibt es auch als E-Book, zum Beispiel bei Amazon*, beim Apple iBook-Store* (Affiliate-Link) oder bei Beam.